Le formule di Erlang sono uno strumento ancora molto utilizzato per calcolare lo staffing nei Call Center, ma esse, come tutti i modelli matematici, comportano obbligatoriamente delle semplificazioni che introducono delle approssimazioni che influenzano l’accuratezza della stima.
Nei casi semplici, dove gli operatori svolgono una singola attività (mono servizio/mono skill) e dove il volume di chiamate è alto e prevedibile, la tecnica matematica di Erlang è sufficiente. Tuttavia, non appena le operazioni del Contact Center diventano più complesse, come ad esempio, con volumi intermittenti, “trabocco” di chiamate tra agent group e presenza di operatori Multi-Skill, le semplificazioni necessarie per continuare ad affidarsi alle formule di Erlang portano all’inevitabile sotto/sovra-dimensionamento degli organici. In pratica, ciò che fa la differenza tra “profitto e perdita“.
Vediamo nello specifico come si comportano le formule di Erlang:
IL CALCOLO BASATO SUL VALOR MEDIO
Per propria natura, le formule di Erlang considerano il flusso delle chiamate offerte sulla base della loro frequenza media di arrivo, come se le chiamate venissero uniformemente distribuite all’interno di ciascun quanto temporale.
Nella realtà, però, le chiamate offerte al call center hanno un comportamento non uniforme all’interno del quanto temporale con dei picchi, dei flessi e dei «null» istantanei. In pratica, ciò che succede è che i KPI target che perdo nei momenti di picco, non posso più recuperarli nei momenti successivi, perché ai picchi seguiranno dei flessi di carico di lavoro o addirittura non arriveranno più chiamate.
Oltre a ciò, le formule di Erlang basano il loro calcolo sul tempo medio di gestione delle chiamate (AHT), che nella realtà è invece variabile da chiamata a chiamata, anche per lo stesso servizio.
Facciamo un esempio:
Considerando che generalmente in un Call Center le misurazioni sono raccolte su intervalli di mezz’ora, prendiamo un intervallo di tale durata e vediamo quale effetto potrebbe avere calcolare la media della frequenza.
Supponiamo un tasso costante di 300 chiamate ogni mezz’ora, una durata media delle chiamate di 180 secondi e come obiettivo un livello di servizio dell’80% con risposta entro 15sec. Applicando le formule di Erlang otterremo che il numero di agenti necessari per raggiungere l’obiettivo è pari a 35 e che questo numero garantirebbe un livello di servizio dell’82%.
Ma cosa succede se smettiamo di considerare che le chiamate siano distribuite in maniera costante all’interno dell’arco temporale di riferimento, così come succede nella realtà?
Supponiamo allora di avere 250 chiamate all’inizio dell’intervallo e di arrivare a 350 alla fine. La media è ancora di 300 chiamate ogni mezz’ora.
Se usiamo le formule di Erlang per analizzare cosa succede minuto per minuto all’interno dell’intervallo otterremo i risultati mostrati nel grafico sottostante:
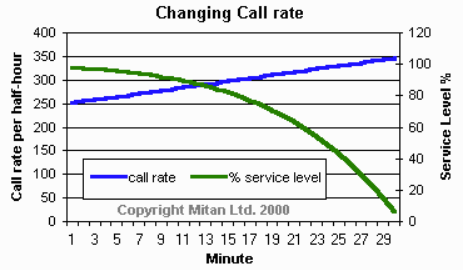
Complessivamente il livello di servizio scende al 69%, rispetto all’82% che ci si sarebbe aspettati.
Poiché, ovviamente, la frequenza delle chiamate varia nel corso della giornata, è fondamentale comprendere e tenere conto dell’errore sopra descritto. L’errore deriva in sintesi dall’utilizzare una frequenza media di chiamate su un intervallo in cui la frequenza nella realtà cambia.
Questo problema non è limitato a Erlang-C, ma si applicherà a qualsiasi formula matematica di gestione delle code che si deciderà di utilizzare.
SOVRACCARICO E LIVELLO DI SERVIZIO
Erlang-C presuppone che il carico di lavoro non superi le capacità degli agenti. In questo contesto, applicare comunque le formule di Erlang potrebbe fornire livelli di servizio o tempi negativi.
ABBANDONI
Le formule di Erlang non possono dire nulla sugli abbandoni in quanto questi dipendono dalla propensione del Cliente all’abbandono (non è uguale per tutti i Clienti) e dal tempo trascorso in coda da ciascuna chiamata.
SOVRASTAFFATURE
In caso di sovraccarico è necessario prevedere una sorta di “valvola di sicurezza” che rimuova alcune chiamate dal sistema. Ad esempio, potrebbe essere impostato un numero massimo di chiamate in attesa (Limited Queue Size) o un tempo massimo di attesa per ciascuna chiamata (Limited Waiting Time). In entrambi i casi Erlang-C tenderà a sottovalutare il livello di servizio che verrà raggiunto e a sovrastimare il numero di agenti necessari per raggiungere il livello di servizio target.
ROUTING DELLE CHIAMATE E TRABOCCHI
Erlang-C presuppone che ci sia una fonte di chiamate gestita da un singolo gruppo di agenti. Tuttavia, la maggior parte dei Call Center fornisce più tipi di servizi attraverso gruppi di agenti organizzati con regole complesse per il “trabocco” o la condivisione di chiamate.
PRIORITA’
Erlang parte dal principio che le chiamate siano gestite secondo la modalità FIFO “primo arrivato, primo servito”. Applicare uno schema di priorità può migliorare notevolmente i livelli di servizio, ma in questo caso sarà indispensabile affidarsi a tecniche di simulazione per stimare correttamente le prestazioni.
SATURAZIONE OPERATORI
Le formule di Erlang non forniscono alcuna informazione previsionale relativamente ai KPI ottenibili con un certo staffing, come ad esempio, la saturazione degli operatori (%Wait) e PMA/h (Produttività Media Agenti) ottenibile con un certo staffing.
COME SUPERARE I LIMITI DELLE FORMULE DI ERLANG?
Loran-P (Pianificazione dei Fabbisogni) è un software che si basa su tecniche di simulazione dinamica che consente il preciso calcolo del fabbisogno di operatori Multi-Skill per quanto temporale tenendo conto contemporaneamente dei seguenti fattori:
- l’arrivo casuale delle chiamate
- la disponibilità di agenti Multi-skill
- la durata variabile del tempo di conversazione
- la probabilità di abbandono delle chiamate in coda
- il valore del livello di servizio obiettivo per ciascun istante temporale
- la saturazione degli operatori obiettivo
- le regole di routing: “trabocchi” o condivisione di chiamate tra gruppi di agenti
COME FUNZIONA LA SIMULAZIONE DINAMICA?
Come sopra descritto, le formule di Erlang presuppongono una frequenza media di arrivo delle chiamate per arco temporale.
Diversamente, la simulazione dinamica riproduce a calcolatore ciò che accade nella realtà, ovvero, l’alternarsi di condizioni di picco, di flesso e di “null” istantanei con abbandoni maggiori negli istanti di picco ed inferiori in quelli di flesso.
Il video mostra chiaramente come, partendo dagli stessi dati, nei due casi si otterranno risultati assai differenti. Infatti, applicando le formule di Erlang si ha la convinzione di garantire un livello di servizio sempre superiore all’80% e un tasso di abbandono quasi nullo. D’altra parte, la simulazione dimostra come il numero di operatori dispiegato sia in realtà insufficiente per rispondere ai volumi offerti nel rispetto del livello di servizio e del tasso di abbandono obiettivo. La saturazione degli operatori risulta quindi inferiore a quella calcolata con le Erlang proprio per effetto dei momenti di flesso o di “null” delle offerte.
Come accennavamo all’inizio è proprio questo che fa la differenza tra “profitto e perdita” nel calcolo dei fabbisogni di organico.